EXCELを用いたスミスチャートの書き方
EXCELを用いたスミスチャートの作成手順
EXCELを用いたスミスチャート描画~導入~
世の中の本を探してみても、スミスチャートの読み方や描き方に関する本や情報はたくさんあります。ただ、実務的には手書きで描くことよりもエクセルを用いて書きたいときや取得したデータを、エクセルを用いてスミスチャートに表現したいことが多いのではないでしょうか。
しかしエクセルの表を見てみてもスミスチャートを選択する項目もなく、自分で描画しようと考えてもあまり情報を得ることができない現実を目の当たりにするのではないでしょうか。そこで、今回はエクセルを用いたスミスチャートの描画方法を解説致します。
スミスチャートはみたことはあるが、詳しい使い方がわからないと言った場合に基本的なところから理解したい人にすすめです。スミスチャートのシミュレーションソフトが付属されておりソフトを使用しながらスミスチャートについて、またインピーダンスの解析方法を学ぶことができます。
スミスチャート描画のEXCELをダウウンロード
実際に下記の手順で作成したEXCELを用いたスミスチャート描画のファイルは下記よりダウンロード頂けます。(ファイルサイズが大きめのためzipで圧縮しています。)
スミスチャートに使用するパラメータ
スミスチャートを描画するにあたり変数について簡単に定義しておきます。
| 変数 | 詳細 |
|---|---|
| \(r\) | 正規化インピーダンス(\(R/Z_O\))の抵抗成分 |
| \(x\) | 正規化インピーダンス(\(X/Z_O\))のリアクタンス成分 |
| \(u\) | 反射係数の実数部 |
| \(v\) | 反射係数の虚数部 |
| \(R\) | 正規化する前の抵抗成分 |
| \(X\) | 正規化する前のリアクタンス成分 |
| \(Z_O\) | 出力インピーダンス(通常\(50Ω\)または\(75Ω\)) |
正規化インピーダンスとは抵抗成分とリアクタンス成分をそのシステム系統の特製インピーダンス\(Z_O\)で割ったものを言います。(\(Z_O\)は主に\(50Ω\)または\(75Ω\)が用いられる系統が多いです。)
スミスチャートの目盛り線の考え方
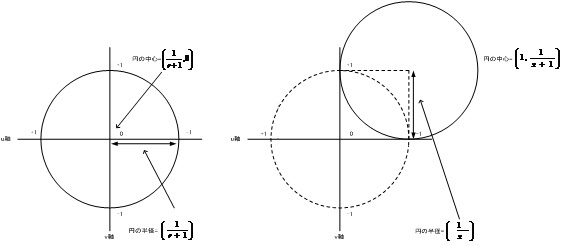
スミスチャートを描画するにあたり、スミスチャートの目盛曲線がどの様な円で描画できるかを簡単に説明します。まず、スミスチャート上では軸をu,vとおいた時、rが一定の値であればxがどれだけ変化しても円の中心が\(1 \over r+1\)で半径も\(1 \over r+1\)の円上にプロットされます。
下記の図の左側が\(r=0\)の場合の円を例として記載しています。次に、\(x\)が一定の値であればどれだけ\(r\)が変化しても円の中心が1で半径が\(1\over x\)の円上にプロットされます。この時\(r=0\)の円の外にある部分は存在しません。\(u\)も\(v\)も\(-1\)~\(+1\)の範囲内に必ずおさまります。
スミスチャートを実際に描画する曲線は?
実際にスミスチャートのフォーマットを作成する場合には下記の定数に対する円を作成する事で大まかなチャートが作成されます。より詳細なチャートを作成したい場合には描画する定数を増やしてゆくと作成できます。まず、\(r\)成分についてプロットしてゆきます
| 定数 | 詳細 |
|---|---|
| \(r=0.0\) | \(x=-∞\)~\(+∞\)の範囲でプロット |
| \(r=0.2\) | \(x=-∞\)~\(+∞\)の範囲でプロット |
| \(r=0.5\) | \(x=-∞\)~\(+∞\)の範囲でプロット |
| \(r=2.0\) | \(x=-∞\)~\(+∞\)の範囲でプロット |
| \(r=5.0\) | \(x=-∞\)~\(+∞\)の範囲でプロット |
次に\(x\)成分についてプロットしてゆきます。
| 定数 | 詳細 |
|---|---|
| \(x=±0.2\) | \(r=0\)~\(+∞\)の範囲でプロット |
| \(x=±0.5\) | \(r=0\)~\(+∞\)の範囲でプロット |
| \(x=±2.0\) | \(r=0\)~\(+∞\)の範囲でプロット |
| \(x=±5.0\) | \(r=0\)~\(+∞\)の範囲でプロット |
上記の線をプロットするとスミスチャートが完成します。
正規化インピーダンスをインピーダンスへ変換
ここでスミスチャートの目盛はこの時点では正規化された反射係数となっている為実際には(グラフから読み取った値)\(×Z_O\)の値がインピーダンスとなります。たとえば
\(Z_O=50Ω\)の場合に\(u=0.5,v=0.2\)の位置の場合に実際の\(R+Xj\)は\((Z_O×u)+(Z_O×v)j=(50×0.5)+(50×0.2)j\),つまり\(25+10j\)となります。
ここで実際に上記の様に実際に\(r\)と\(x\)をプロットしようとした時に、実際には横軸が\(u\)、縦軸が\(v\)となっているため直接プロットしてゆくことができないことに気付くかと思います。
そこで実際にスミスチャートの目盛曲線を描画するためには、\(r\)と\(x\)を反射係数の実数部\(U\)と反射係数の虚数部\(V\)へ変換してプロットして行く必要があります。この変換の計算については「反射係数の計算式」に詳しく記載していますので参照頂くとわかると思うのですが、結果として、
となります。これでエクセルにスミスチャートを描画する準備ができました。
エクセルへの描画の手順~表の作成~
まず\(x\)または\(r\)が一定のときにそれぞれ\(x\)または\(r\)を「∞」まで変化させてゆき,そのときの\(U\)と\(V\)の値をプロットして行くのですが、ここでどの様なレンジで代入して行けばよいか解らないかと思います。
スミスチャートは\(x\)または\(r\)が小さいほど目盛が広くなっているため、小さい値ほど多くのプロット数が必要となり値が大きくなるほどプロットは荒くしてゆきます。実際には下記のレンジでプロットすると曲線をきれいに引く事ができます。
\(r\)を一定にし、\(x\)を変化させる
\(r\)が一定の値のときに\(x\)を変化させた下記の表の8個の曲線(円)を描きます。
| \(r\) | \(x\)の範囲が下記の間 | \(x\)をプロットする間隔 |
|---|---|---|
| \(r=0\) | \(x=0\)~\(±1\)までの範囲 | \(0.05\)刻み |
| \(r=0\) | \(x=±1\)~\(±2\)までの範囲 | \(0.10\)刻み |
| \(r=0\) | \(x=±2\)~\(±3\)までの範囲 | \(0.20\)刻み |
| \(r=0\) | \(x=±3\)~\(±4\)までの範囲 | \(0.50\)刻み\((±3.00/±3.50/±4.00\)の6点) |
| \(r=0\) | \(x=±4\)~\(±10\)までの範囲 | \(1.00\)刻み |
| \(r=0\) | \(x=±10\)~\(±100\)までの範囲 | \(10.00\)刻み |
| \(r=0\) | \(x=±100\)~\(±1000\)までの範囲 | \(±1000\)の点のみ |
| \(r=0\) | \(x=±1000\)~\(±10000\)までの範囲 | \(±10000\)の点のみ(この点を\(±∞\)とみなす) |
上記の手順でエクセルに\(r\)と\(x\)を入力した表を作成したら、次にそれぞれのポイントでの反射係数の実数部\(U\)と反射係数の虚数部\(V\)の列を作成します。下記のその例を掲載致します。
下記の画像では式を見える様に表記していますので実際は各行にあわせこの式を入力して下さい。また、\(r\)と\(x\)を変化させてゆく部分は途中を省略して表記していますが、実際は全て入力して下さい。反射係数が何か知りたいと言うかたは反射係数の計算式をご覧下さい。

\(x\)を一定にし、\(r\)を変化させる
\(x\)が一定の値のときに\(r\)を変化させた下記の表の9個の曲線を描きます。
| \(x\) | \(r\)の範囲が下記の間 | \(r\)をプロットする間隔 |
|---|---|---|
| \(x=0.2\) | \(r=0\)~\(+1\)までの範囲 | \(0.05\)刻み |
| \(x=0.2\) | \(r=+1\)~\(+2\)までの範囲 | \(0.10\)刻み |
| \(x=0.2\) | \(r=+2\)~\(+3\)までの範囲 | \(0.20\)刻み |
| \(x=0.2\) | \(r=+3\)~\(+4\)までの範囲 | \(0.50\)刻み\((+3.00/+3.50/+4.00\)の3点) |
| \(x=0.2\) | \(r=+4\)~\(+10\)までの範囲 | \(1.00\)刻み |
| \(x=0.2\) | \(r=+10\)~\(+100\)までの範囲 | \(10.00\)刻み |
| \(x=0.2\) | \(r=+100\)~\(+1000\)までの範囲 | \(+1000\)の点のみ |
| \(x=0.2\) | \(r=+1000\)~\(+10000\)までの範囲 | \(+10000\)の点のみ(この点を\(∞\)とみなす) |
上記の手順でエクセルに\(r\)と\(x\)を入力した表を作成したら、次にそれぞれのポイントでの反射係数の実数部\(U\)と反射係数の虚数部\(V\)の列を作成します。下記のその例を掲載致します。
下記の画像では式を見える様に表記していますので実際は各行にあわせこの式を入力して下さい。また、\(r\)と\(x\)を変化させてゆく部分は途中を省略して表記していますが、実際は全て入力して下さい。

実際のエクセルへの描画の手順~表の作成~
上記の様にそれぞれ値を一定にした場合の\(r\)と\(x\)と\(U\)と\(V\)の表を作成し計16種類の表を作成すると下記の様に表ができあがります。表が多いため一部を抜粋すると下記の画像の様な表ができます。
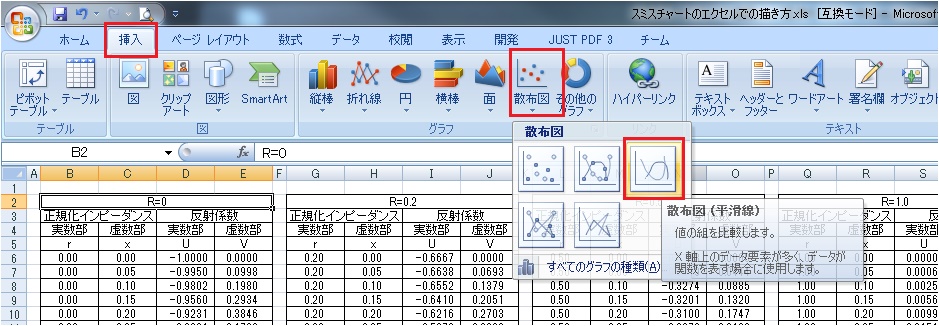
次に特にセルはどこでも構いませんので、挿入のタブをクリックし、散布図を選択します。すると5種類の散布図の選択画面が出てきますので、散布図(平滑線)を選択しクリックします。
すると下記の様なグラフが挿入されます。
実際のエクセルへの描画の手順~グラフの作成~
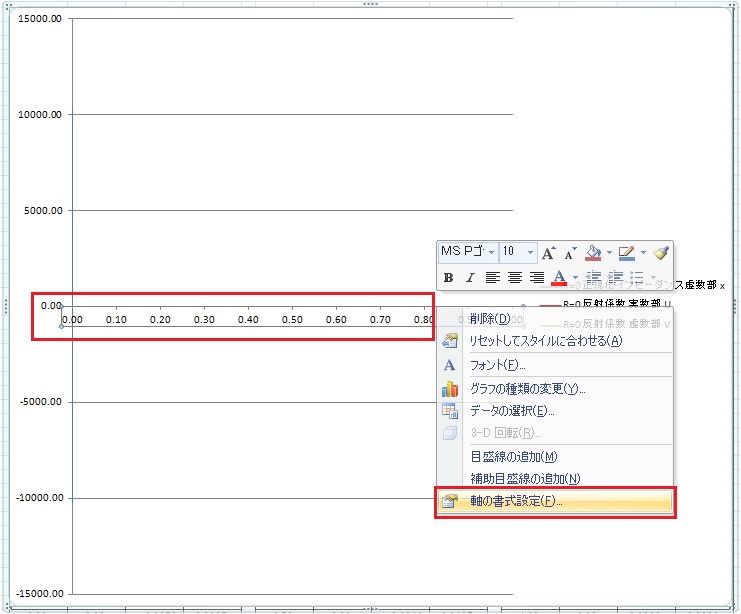
ただこの状態ではスミスチャートのメモリの状態とは異なりますので少し変更してゆきます。ます横軸のメモリの部分をクリックしてさらに軸の書式の設定をクリックして設定を行います。
スミスチャートの軸は中心が0となるために中心が0となる様に変更し、また最大値が1または±1なので±1になる様に設定します。具体的な設定は下記の画面の様に設定します。
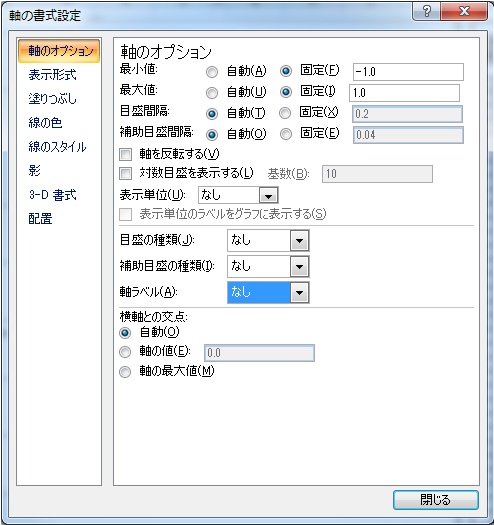
この作業を縦軸に対しても同様に行います。
次に、この時点で表示されている不要なメモリと線を選択し「Delete」キーで削除してゆきます。一度削除しても他の線がのこる場合にはその線も消してゆきます。すると下の様に何もないグラフのボックスが出来上がります。
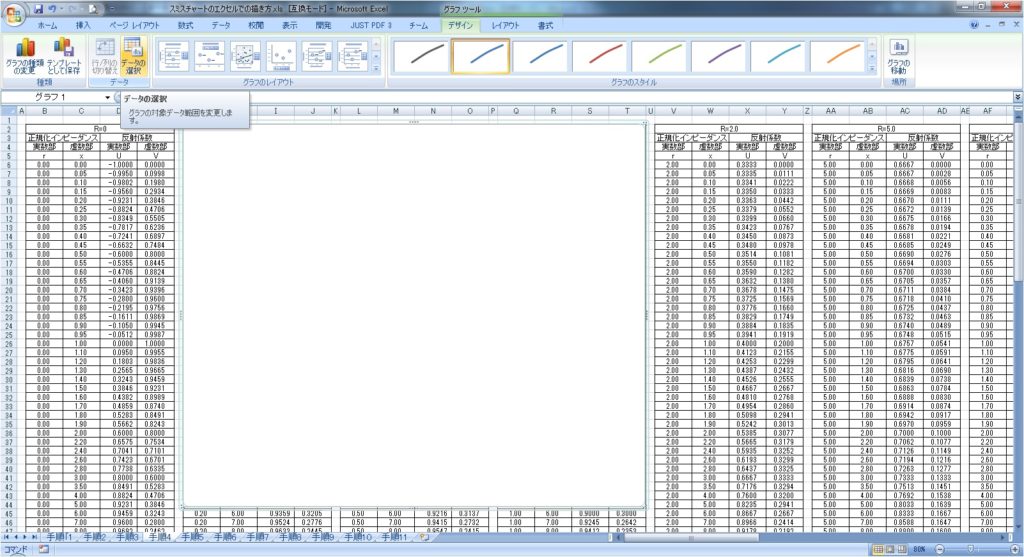
次にこのグラフのボックスに曲線を描画してゆきます。まず、ボックス内で右クリックをしてデータの選択をクリックしてください。
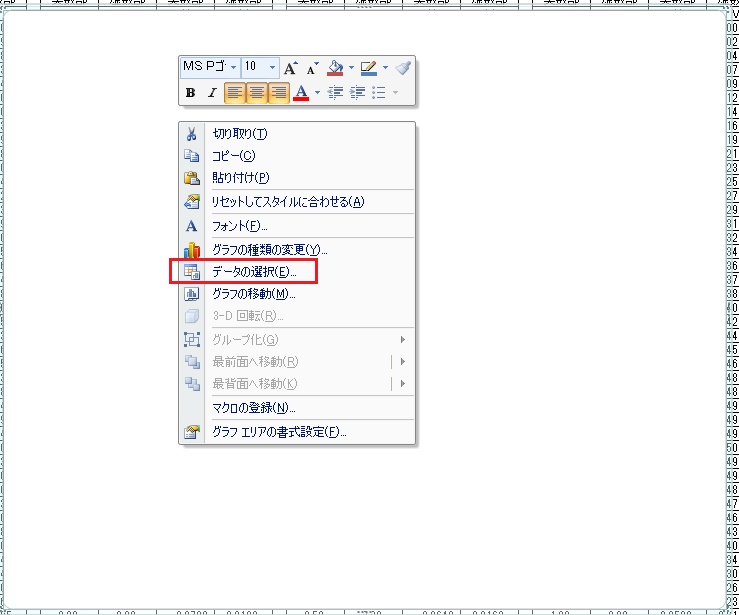
下記の様画面がでてくるので、「追加」のボタンを押してください。
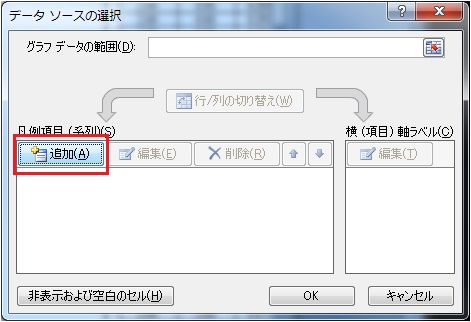
すると下記の様な画面がでてきますので下記の様にそれぞれセルを選択してください。
| 系列名(N): | 「R=0」や「R=0.2」または「X=0」や「X=0.2」、「X=-0.2」等の曲線名のセル |
| 系列Xの値(X): | 実数部Uの列の数値の範囲を選択 |
| 系列Yの値(Y): | 虚数部Vの列の数値の範囲を選択 |
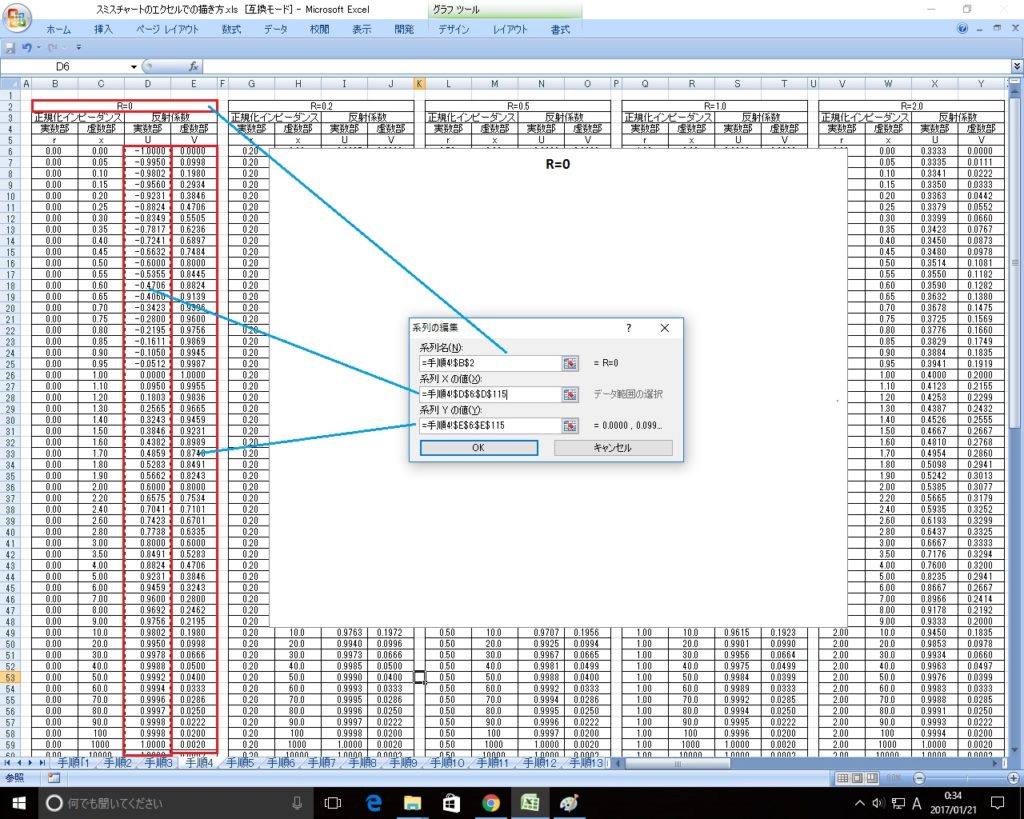
すると下記の様にこれでまず\(r=0\)の曲線が描画されました。
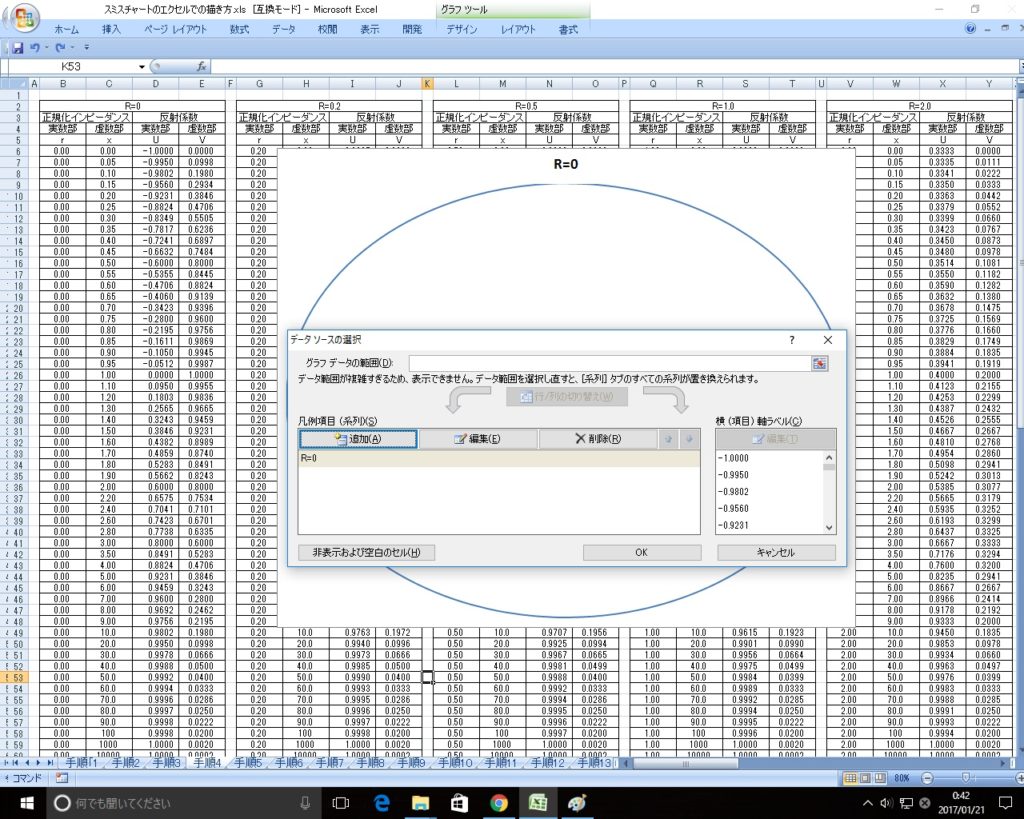
上記の曲線の追加の作業をすべての\(r\)と\(x\)に対して(計17曲線)繰り返してゆきます。
するとすべての線を引いた状態が下記の様になります。
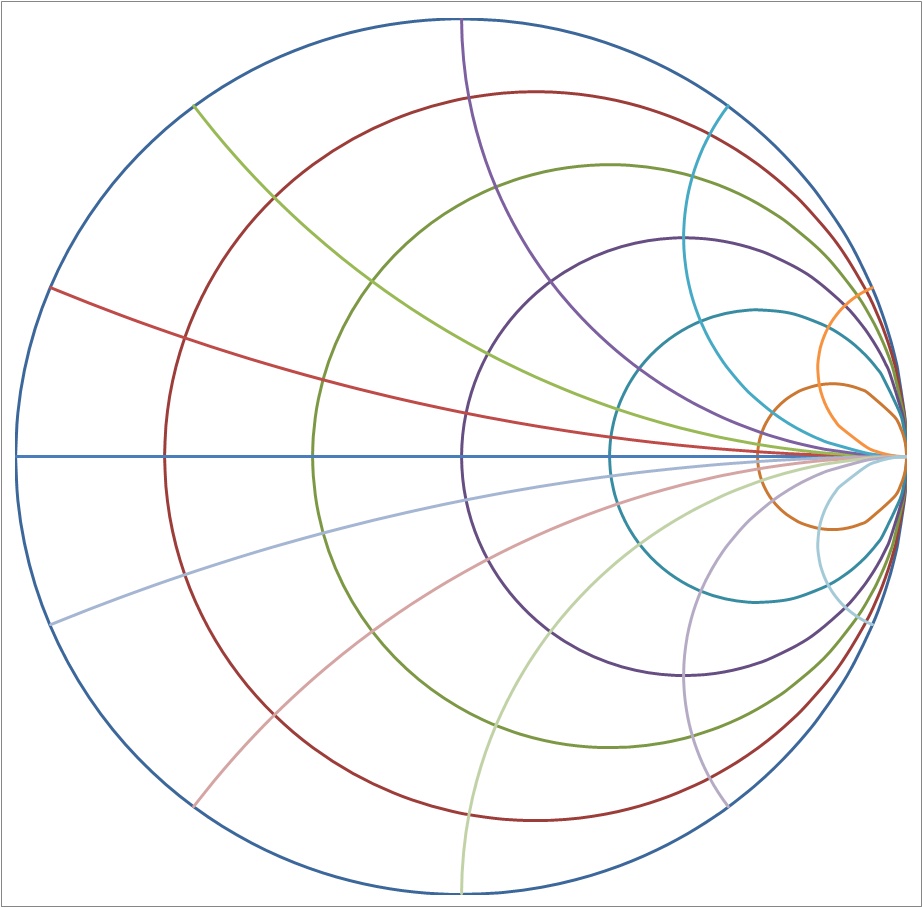
グラフの形を整える
上記の状態ではまだスミスチャートとしてきれいな形ではないので、各線を右クリックしてデータ系列の書式の設定等で線の色を変えたり、テキストボックスで目盛りを追加したりして、体裁を整えると下記の様になります。
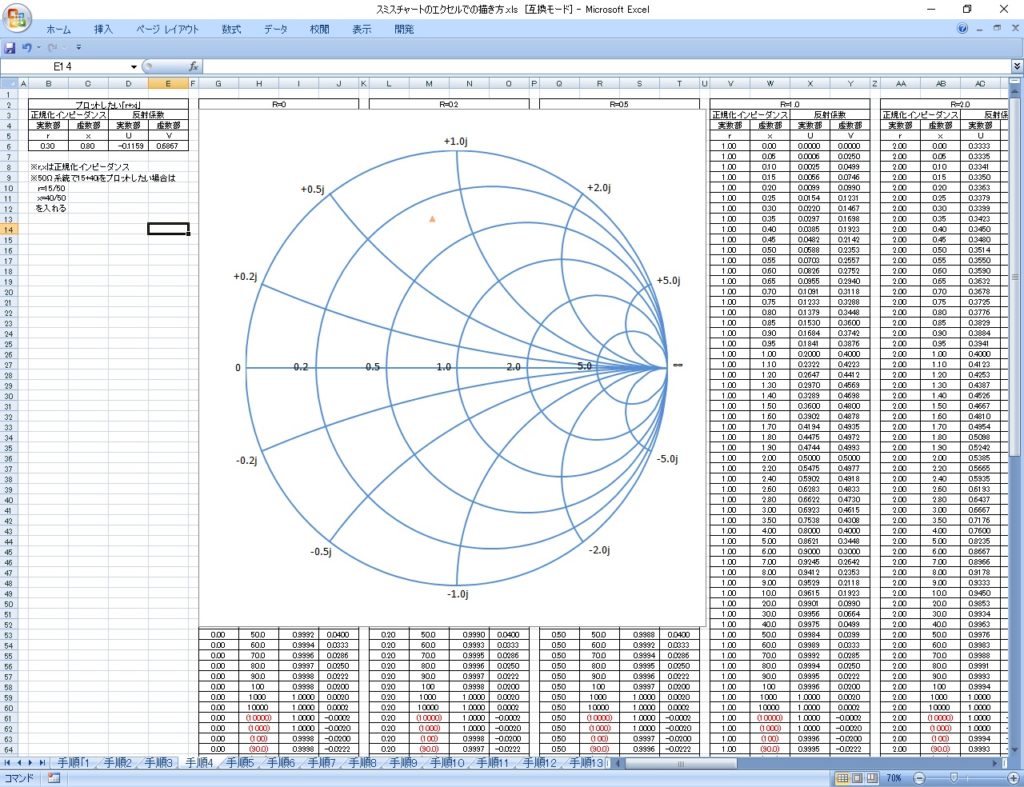
この時、1点のプロットも打てるようにデータ系列も追加するなどすると下記の様なスミスチャートが出来上がります。