コンデンサのリアクタンス
コンデンサのリアクタンスとは?
コンデンサのリアクタンスの概要
コンデンサは日本ではそう呼ばれていますが、海外などでは通常キャパシターと呼ばれています。基本的にコンデンサの構造は2枚の平行な金属を並べられたものであり、その間は導電性の無い空気や誘電体がはさまれているため、基本的に直流に対しての抵抗値は「∞」とみなすことができます。
このコンデンサには電池の様に電気をためる性質がありその成分をキャパシタンスと呼びます。このキャパシタンスの成分から、コンデンサのリアクタンスと呼ばれる値が求められます。キャパシタンスは電圧に対して電流を90°進める性質があるのですが、キャパシタンスから求められるリアクタンスは電流を90°進めるときにどれだけの電流の大きさで進めるかを抵抗と電圧から電流を求める様に、リアクタンスと電圧からすすめる電流の大きさを表現できる様に疑似的な抵抗の様な意味合いを持たせた成分イメージして頂ければわかりやすいかと思います。
キャパシタンスの場合には電流を押し戻す強さとなりますが、コイルのインダクタンスの場合には逆にこのリアクタンスが正の値となりどれだけの大きさで電流を90°遅れさせるかを表すことになります。
もうすこし詳しくコンデンサの特性やその他コンデンサについて勉強してみたいと言うかたはこの本を参考にしてみて下さい。素子の構造や動作原理,応用回路例,使用上の注意といった実用的な内容から実際に回路の設計や専門的な計算に関わる応用まで分かりやすく解説されています。
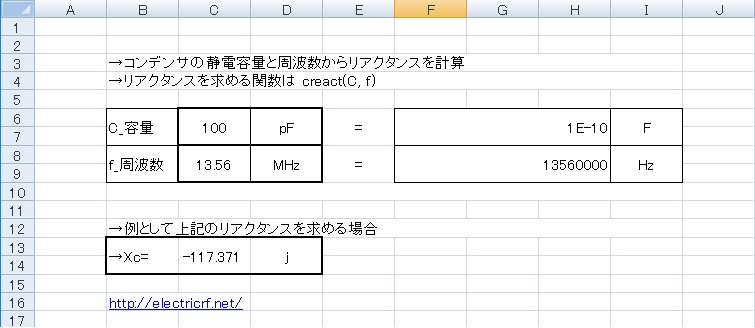
容量性リアクタンスの計算式EXCELをダウンロード
このページで紹介する容量性リアクタンスの計算式のプログラムをエクセルの標準モジュールへ記入し、関数として使用できるフォーマットにしました。下記よりダウンロードいただけますのでご利用下さい。2次配布、改変等も問題御座いませんのでぜひお役だて下さい。
コンデンサのキャパシタンス
ここで抵抗の電気的な機能は一般的によく聞くことのある「\(R[Ω]\)(オーム)」の単位で表され、またコイル(インダクター)の電気的な機能は「\(L[H]\)(ヘンリー)」の単位で表される様に、コンデンサはキャパシタンス「\(C[F]\)(ファラド)」の単位で表されます。
コンデンサは直流は通過しませんが交流をになると、電力が通過する特性をもっています。しかしこのときに、コンデンサの容量によってその度合いは異なりますが、電圧よりも電流が進んで先に出てくる現象が現れます。
簡単にイメージをするならコンデンサによって電流が引っ張られているイメージをもっていただけると分かりやすいのではないでしょうか。
コンデンサによる電圧と電流の関係
コンデンサによって電流が引っ張られているイメージと言いましたが、実際にはどの様なものであるか、下記にもう少し詳しくその電圧と電流の関係性を示しておきます。下の図はサイン波形の電力なのですが、コンデンサのキャパシタンスにより電流の位相が90°進んでいる場合の図です。
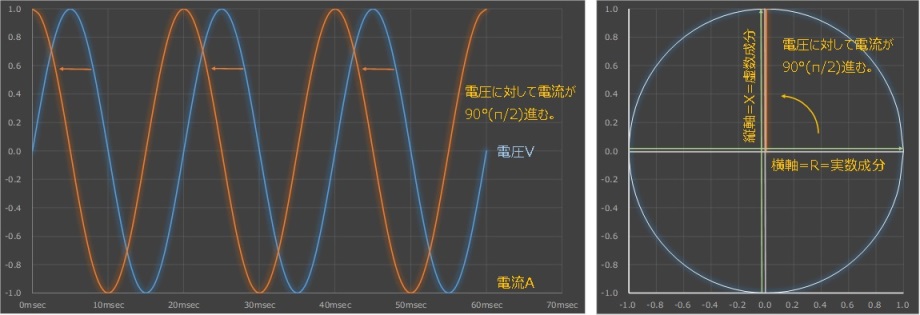
この電流の進みはコンデンサだけであれば90°なのですが抵抗と組み合わせて使用することによってキャパシタンス「\(C\)」や交流の周波数に依存してその回路全体の遅れの角度が変化してきます。
上記を踏まえたうえで、コンデンサから出てくる交流電圧\(V\)と電流\(I\)の関係は下記の様な式で表現することができます。
$$I = {V \times j \times ω \times C}$$
上記の式は電圧と電流のみではなく、その位相を含めて表現した形となります。この場合発生している電流の位相は電圧に対して90°ずれている状態となっています。
| 変数 | 詳細 |
|---|---|
| \(I\) | 電流[\(A\)] |
| \(V\) | 電圧[\(V\)] |
| \(j\) | 虚数(今回の場合位相というイメージ) |
| \(π\) | 円周率\(≒3.14\) |
| \(f\) | 周波数[\(Hz\)] |
| \(ω\) | 角速度[\(rad/s\)]\(=2×π×f\) |
| \(C\) | キャパシタンス[\(F\)] |
コンデンサのリアクタンスと抵抗の違いは?
上記の式を電圧\(V\)と電流\(I\)の比をとるかたちに変形すると下記の様に変形することができます。
$${V \over I} = {1 \over jωC}$$この式を複素数\(j\)について有利化すると$${V \over I} = {{1 \over jωC} \times {j \over j}=-{1 \over ωC}j}$$となり、この時の電圧\(V\)と電流\(I\)の比である「\(V/I\)」がリアクタンスと呼ばれています。このページの上部で疑似的な抵抗と表現しましたが、それはどういうことでしょうか。
ここで式を見ていただければわかると思うのですが、電流と電圧の関係が、通常のオームの法則「\(V=RI\)」つまり「\(V/I=R\)」と同じ形となっていることがわかります。
この\(-{1 \over ωC}\)は電気抵抗を表す「\(R\)」と似た様な意味をもちますが、実際は電流、電圧と位相が90°ずれた状態を含めた疑似的な抵抗を表し「\(X\)」の記号が用いられ、単位は抵抗と同じ「\(Ω\)」を使用します。ただしあくまで疑似的な抵抗を表しているため、抵抗の様に実際に電力を消費することはありません。
この疑似的な抵抗を通常の抵抗と区別するため虚数で一般的に表されます。なぜ虚数をもちいるかと言うとこれは位相のみを表しており実際の抵抗と組み合わされて初めて意味を持ちます。抵抗に流れる電流に対してどれだけ電流が遅れて発生するか位相は角度で表されるため、360°までしかありません。このためベクトルで計算すると都合がよく、そのベクトルでの計算は虚数で表すことによって簡単に行うことができるためです。
コンデンサのリアクタンス計算式のまとめ
コンデンサのリアクタンスは容量性リアクタンスともよばれていますが、その容量性リアクタンスであることを分かりやすくするために「\(X\)」に「\(_C\)」をつけて区別することが多いです。ここでこれまでのまとめとして誘導性リアクタンスの計算式を記載しておきます。
| 変数 | 詳細 |
|---|---|
| \(X_C\) | 容量性リアクタンス[\(Ω\)] |
| \(Z\) | インピーダンス[\(Ω\)] |
| \(R\) | 抵抗[\(Ω\)] |
とすると\(X_C=-{1 \over ωC}\)となります。そして通常、インピーダンス「\(Z\)」は\(Z=R-X_C j\)の形であらわされ、容量性リアクタンス(コンデンサの場合)にはこの「\(X_C\)」は上記のマイナスの符号となります。
容量性リアクタンスの計算プログラム
容量性リアクタンスの計算を簡単に行うことができる様にコードを作成しましたので参考までに掲載しておきます。
| 変数 | 詳細 |
|---|---|
| L1 | コンデンサのキャパシタンス[\(C]\) |
| HZ | 交流の周波数[\(Hz\)] |
EXCELの標準モジュールへ下記をコピペしていただくとエクセルの関数として利用頂けます。
Public Function creact(C1 As Double, HZ As Double) As Double
If C1 <= 0 Then
creact = 0
ElseIf HZ <= 0 Then
creact = 0
Else
creact = -1 / (2 * Application.WorksheetFunction.Pi * HZ * C1)
End If
End Function