インピーダンスの並列合成の計算式
インピーダンスの並列合成
インピーダンスの並列合成~導入~
通常の抵抗の並列合成であれば、和分の積\((R_a×R_b)/(R_a+R_b)\)で簡単に求める事ができます。しかし虚数の成分が入ってくるインピーダンスを計算する場合は簡単には行きません。考え方としては和分の積\((Z_a×Z_b)/(Z_a+Z_b)\)で求める事には間違えないのですがこの\(Z_a\)と\(Z_b\)は\(r+xj\)と言う虚数の成分を含むため計算が複雑になります。
いろいろなサイトや本をみても\(Z_a,Z_b\)の片方が虚数のみの場合、両方が虚数の場合の計算の方法の記載は多くすぐに見つかるのですが両方が実数と虚数を含む場合の計算方法が示されていることは少ないです。そこで\(Z_a,Z_b\)ともに\(r+xj\)の形をとる場合の並列合成の計算の方法を紹介致します。(片方が実数のみの場合には\(x=0\)や\(r=0\)とすることでどのパターンにも応用できます。)
インピーダンスについてフーリエ変換やラプラス変換といった難しい計算を避けながら、数式のもつ意味から丁寧に説明されている本です。少し高価な本ではありますが実際のインピーダンスの測定の結果の解釈方法が説明されておりこの本を理解することで電気的な現象とインピーダンスとの関係性の理解が非常に深まります。
インピーダンスの並列合成の計算式EXCELフォーマット
このページで紹介するインピーダンスの並列合成の計算式をエクセルのフォーマットにしました。下記よりダウンロードいただけますのでご利用下さい。2次配布、改変等も問題御座いませんのでぜひお役だて下さい。

抵抗の並列合成の計算式
ここで上記でものべましたが抵抗の並列合成の計算式を記載しておきます。虚数成分を含むインピーダンスの並列合成の場合にもこの考え方が基本となります。下記の様に\(R_a\)[\(Ω\)]と\(R_b\)[\(Ω\)]を並列に合成した場合の抵抗\(R_c\)[\(Ω\)]を求める場合を考えます。
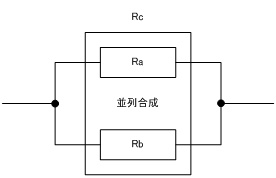
この時に並列合成後の抵抗\(R_c\)[\(Ω\)]は下記の式で表すことができます。
$$R_c={R_a \times R_b \over {R_a+R_b}}$$
| 変数 | 詳細 |
|---|---|
| \(R_a\) | 合成される抵抗[\(Ω\)] |
| \(R_b\) | 合成される抵抗[\(Ω\)] |
| \(R_c\) | \(R_a\)と\(R_b\)を合成した抵抗[\(Ω\)] |
インピーダンスの並列合成の複素数計算式
上記の式の「\(Z_a\)」,「\(Z_b\)」,「\(Z_c\)」にそれぞれインピーダンスの実数部と虚数部を分けた\(R+Xj\)の形へ代入すると、
$$R_c+X_c j={{(R_a+X_a j) \times (R_b+X_b j)} \over (R_a+X_a j)+(R_b+X_b j)} $$
となります。この式をさらに整理すると、
$$R_c+X_c j={{(R_a・R_b-X_a・X_b)+(R_a・X_b+R_b・X_a)j} \over (R_a+R_b)+(X_a +X_b)j} $$
となります。ここでこの式の複素数を有理化してゆく必要があるのですが式が非常に複雑になるため、まず下記の様に「\(A\)」,「\(B\)」,「\(C\)」,「\(D\)」とおき計算を簡略化します。
$$A=(R_a・R_b-X_a・X_b)$$$$B=(R_a・X_b+R_b・X_a)$$$$C=(R_a+R_b)$$$$D=(X_a+X_b)$$この「\(A\)」,「\(B\)」,「\(C\)」,「\(D\)」を前述の式に代入すると、
$${A+Bj \over C+Dj}={(A+Bj)・(C-Dj) \over (C+Dj)・(C-Dj)}$$これを整理すると$${A+Bj \over C+Dj}={(A・C+B・D)+(B・C-A・D)j \over C^2+D^2}$$と有利化することができます。有利化の詳細につきましては「複素数の有理化」を参照して下さい。
ここで「\(A\)」,「\(B\)」,「\(C\)」,「\(D\)」と置き換えた内容をもとの式へ戻してゆきます。それぞれにもとの値を代入すると、
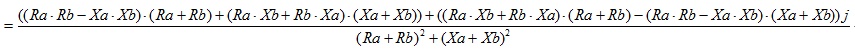
となり、この式を実数成分と虚数成分へ分けると、
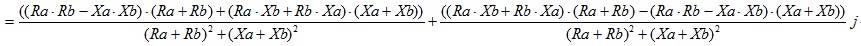
となります。数式が長すぎるので左辺は省略していますが上記の計算で左辺は、$$R_c+X_c j$$であることから上記の長い式の実数成分が\(R_c\)となり虚数成分が\(X_c j\)となることがわかります。つまり\(Z_c=R_c+X_c j\)の\(R_c\)と\(X_c\)は下記の様になります。
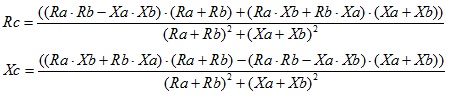
非常に長い式ですが,いずれかの\(R,X\)が\(0\)の場合には式を簡略化することができます。
インピーダンスの並列合成プログラム
インピーダンスの並列合成の計算を簡単に行うことができる様にコードを作成しましたので参考までに掲載しておきます。
| 変数 | 詳細 |
|---|---|
| \(R1\) | 合成されるインピーダンス\(Z1\)の実数部[\(Ω\)] |
| \(X1\) | 合成されるインピーダンス\(Z1\)の虚数部[\(Ω\)] |
| \(R2\) | 合成されるインピーダンス\(Z2\)の実数部[\(Ω\)] |
| \(X2\) | 合成されるインピーダンス\(Z2\)の虚数部[\(Ω\)] |
EXCELの標準モジュールへ下記をコピペしていただくとエクセルの関数として利用頂けます。
並列合成の実数部の計算
Public Function prcombr(R1 As Double, X1 As Double, R2 As Double, X2 As Double) As Double
Dim A As Double
Dim B As Double
Dim C As Double
Dim D As Double
A = (R1 * R2) - (X1 * X2)
B = (R1 * X2) + (R2 * X1)
C = (R1 + R2)
D = (X1 + X2)
If C <= 0 Then prcombr = 0 ElseIf R1 <> 0 And R2 = 0 And X1 = 0 And X2 = 0 Then
prcombr = R1
ElseIf R1 = 0 And R2 <> 0 And X1 = 0 And X2 = 0 Then
prcombr = R1
Else
prcombr = ((A * C) + (B * D)) / ((C ^ 2) + (D ^ 2))
End If
End Function並列合成の実数部の計算
Public Function prcombx(R1 As Double, X1 As Double, R2 As Double, X2 As Double) As Double
Dim A As Double
Dim B As Double
Dim C As Double
Dim D As Double
A = (R1 * R2) - (X1 * X2)
B = (R1 * X2) + (R2 * X1)
C = (R1 + R2)
D = (X1 + X2)
If X1 = 0 And X2 = 0 Then
prcombx = 0
ElseIf X1 <> 0 And X2 = 0 And R1 = 0 And R2 = 0 Then
prcombx = R1
ElseIf X1 = 0 And X2 <> 0 And R1 = 0 And R2 = 0 Then
prcombx = R1
Else
prcombx = ((B * C) - (A * D)) / ((C ^ 2) + (D ^ 2))
End If
End Function